Mengenal Dunia Bentuk: Panduan Lengkap Soal Bangun Datar dan Bangun Ruang untuk Kelas 3 SD

Dunia di sekitar kita penuh dengan berbagai bentuk. Dari meja makan berbentuk persegi panjang, roda sepeda yang bulat, hingga kotak pensil yang menyerupai balok, semuanya adalah manifestasi dari konsep bangun datar dan bangun ruang. Bagi siswa kelas 3 Sekolah Dasar, pemahaman awal tentang bentuk-bentuk ini merupakan fondasi penting dalam perkembangan kemampuan spasial, logika, dan pemecahan masalah.

Artikel ini akan membahas secara mendalam mengenai soal-soal bangun datar dan bangun ruang yang lazim ditemui di kelas 3 SD. Kita akan mengupas tuntas materi, memberikan contoh soal beserta pembahasannya, serta tips agar siswa lebih mudah memahami dan menguasainya. Tujuannya adalah agar guru dan orang tua dapat membimbing anak-anak dengan efektif dalam menjelajahi dunia bentuk ini.

Bagian 1: Memahami Bangun Datar – Fondasi Dunia Bentuk

Bangun datar adalah bangun dua dimensi yang hanya memiliki panjang dan lebar, serta dibatasi oleh garis lurus atau lengkung. Siswa kelas 3 biasanya dikenalkan dengan beberapa bangun datar dasar, yaitu:

1. Persegi: Bangun datar dengan empat sisi sama panjang dan empat sudut siku-siku (90 derajat).

   • Sifat-sifat: Memiliki 4 sisi sama panjang, 4 sudut siku-siku, 2 diagonal yang sama panjang dan saling tegak lurus.
   • Contoh benda: Ubin lantai, daun pintu, bingkai foto.

2. Persegi Panjang: Bangun datar dengan dua pasang sisi berhadapan sama panjang dan empat sudut siku-siku.

   • Sifat-sifat: Memiliki 2 pasang sisi berhadapan sama panjang, 4 sudut siku-siku, 2 diagonal yang sama panjang.
   • Contoh benda: Buku tulis, layar televisi, lapangan sepak bola.

3. Segitiga: Bangun datar dengan tiga sisi dan tiga sudut. Segitiga memiliki berbagai jenis berdasarkan panjang sisinya (sama sisi, sama kaki, sembarang) dan besar sudutnya (siku-siku, lancip, tumpul). Untuk kelas 3, fokus umumnya pada segitiga secara umum dan segitiga siku-siku.

   • Sifat-sifat: Memiliki 3 sisi, 3 sudut. Jumlah ketiga sudutnya selalu 180 derajat.
   • Contoh benda: Atap rumah (model sederhana), potongan pizza, rambu lalu lintas.

4. Lingkaran: Bangun datar yang semua titik pada kelilingnya berjarak sama dari titik pusatnya.

   • Sifat-sifat: Tidak memiliki sudut, memiliki titik pusat, memiliki jari-jari dan diameter.
   • Contoh benda: Roda, jam dinding, koin.

Konsep yang Diajarkan pada Bangun Datar Kelas 3:

• Identifikasi Nama Bangun Datar: Siswa belajar mengenali dan menyebutkan nama bangun datar berdasarkan bentuknya.
• Menghitung Jumlah Sisi dan Sudut: Siswa mampu menghitung jumlah sisi dan sudut pada bangun datar.
• Sifat-sifat Dasar Bangun Datar: Memahami perbedaan antara persegi, persegi panjang, segitiga, dan lingkaran.
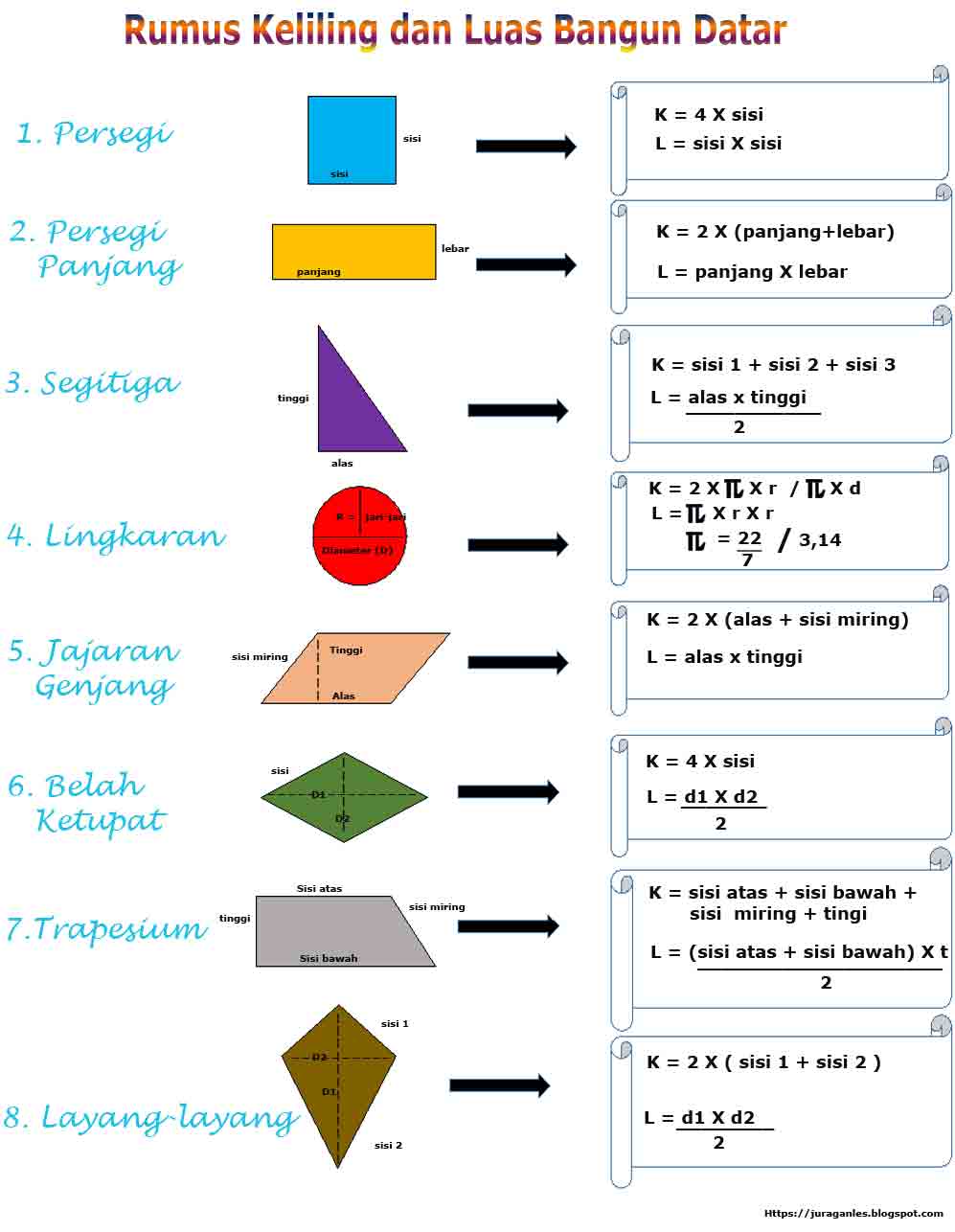
• Keliling Bangun Datar: Konsep dasar keliling adalah jumlah panjang semua sisi bangun datar. Rumus yang diajarkan biasanya masih bersifat deskriptif (misalnya, keliling persegi panjang adalah panjang + lebar + panjang + lebar). Pengenalan rumus formal mungkin baru diperdalam di kelas selanjutnya.
• Luas Bangun Datar: Konsep dasar luas adalah area yang ditutupi oleh bangun datar tersebut. Untuk kelas 3, biasanya diperkenalkan melalui penghitungan menggunakan satuan tidak baku (misalnya, berapa banyak persegi kecil yang menutupi permukaan). Rumus formal luas persegi (s x s) dan luas persegi panjang (p x l) mulai diperkenalkan secara sederhana.

Contoh Soal Bangun Datar Kelas 3 Beserta Pembahasan:

Soal 1 (Identifikasi dan Sifat):
Perhatikan gambar bangun datar berikut.

Sebutkan nama setiap bangun datar tersebut dan tuliskan salah satu sifatnya!

• Pembahasan:
  • Bangun A adalah Persegi. Sifatnya: memiliki empat sisi sama panjang.
  • Bangun B adalah Persegi Panjang. Sifatnya: memiliki dua pasang sisi berhadapan sama panjang.
  • Bangun C adalah Segitiga. Sifatnya: memiliki tiga sisi.
  • Bangun D adalah Lingkaran. Sifatnya: tidak memiliki sudut.

Soal 2 (Menghitung Sisi dan Sudut):
Berapa jumlah sisi dan sudut yang dimiliki oleh bangun datar persegi panjang?

• Pembahasan:
  Bangun datar persegi panjang memiliki 4 sisi dan 4 sudut.

Soal 3 (Keliling Sederhana):
Sebuah taman bermain berbentuk persegi panjang memiliki panjang 5 meter dan lebar 3 meter. Berapa meter keliling taman bermain tersebut?

• Pembahasan:
  Keliling persegi panjang adalah jumlah semua sisinya.
  Keliling = panjang + lebar + panjang + lebar
  Keliling = 5 meter + 3 meter + 5 meter + 3 meter
  Keliling = 16 meter.
  Atau menggunakan rumus sederhana: Keliling = 2 x (panjang + lebar) = 2 x (5 + 3) = 2 x 8 = 16 meter.

Soal 4 (Luas dengan Satuan Tidak Baku):
Selembar kertas berbentuk persegi panjang ditutupi oleh ubin-ubin kecil berbentuk persegi. Jika ada 12 ubin persegi yang menutupi seluruh permukaan kertas tersebut, berapa luas kertas tersebut jika diukur dengan satuan ubin persegi?

• Pembahasan:
  Luas kertas tersebut adalah jumlah ubin persegi yang menutupi permukaannya.
  Luas = 12 ubin persegi.

Soal 5 (Luas Persegi Sederhana):
Sebuah ubin lantai berbentuk persegi memiliki panjang sisi 10 cm. Berapa luas ubin lantai tersebut?

• Pembahasan:
  Luas persegi = sisi x sisi
  Luas = 10 cm x 10 cm
  Luas = 100 cm².

Bagian 2: Menjelajahi Ruang dengan Bangun Ruang

Bangun ruang adalah bangun tiga dimensi yang memiliki volume (isi) dan dapat menempati ruang. Siswa kelas 3 diperkenalkan dengan beberapa bangun ruang dasar, yang sering kali terkait dengan benda-benda di sekitar mereka.

1. Kubus: Bangun ruang yang dibatasi oleh enam sisi berbentuk persegi yang sama besar.

   • Sifat-sifat: Memiliki 6 sisi berbentuk persegi, 12 rusuk sama panjang, 8 titik sudut.
   • Contoh benda: Dadu, kotak kado berbentuk kubus, rubik.

2. Balok: Bangun ruang yang dibatasi oleh enam sisi berbentuk persegi panjang.

   • Sifat-sifat: Memiliki 6 sisi berbentuk persegi panjang, 12 rusuk (terdiri dari 3 pasang rusuk yang sama panjang), 8 titik sudut.
   • Contoh benda: Buku, lemari, kulkas, kotak sepatu.

3. Tabung: Bangun ruang yang memiliki alas dan tutup berbentuk lingkaran yang sama, serta sisi tegak yang melengkung.

   • Sifat-sifat: Memiliki 2 sisi alas dan tutup berbentuk lingkaran, 1 sisi tegak melengkung, tidak memiliki rusuk lurus dan titik sudut.
   • Contoh benda: Gelas, kaleng minuman, pipa.

4. Kerucut: Bangun ruang yang memiliki alas berbentuk lingkaran dan sebuah titik puncak (apex).

   • Sifat-sifat: Memiliki 1 sisi alas berbentuk lingkaran, 1 sisi selimut melengkung, 1 titik puncak, 1 rusuk lengkung.
   • Contoh benda: Topi ulang tahun, corong, nasi tumpeng.

5. Bola: Bangun ruang yang semua titik permukaannya berjarak sama dari titik pusatnya.

   • Sifat-sifat: Hanya memiliki 1 sisi lengkung, tidak memiliki rusuk dan titik sudut.
   • Contoh benda: Bola basket, bola sepak, kelereng.

Konsep yang Diajarkan pada Bangun Ruang Kelas 3:

• Identifikasi Nama Bangun Ruang: Siswa belajar mengenali dan menyebutkan nama bangun ruang berdasarkan bentuknya.
• Menghitung Jumlah Sisi, Rusuk, dan Titik Sudut: Ini adalah keterampilan kunci. Siswa belajar membedakan mana yang disebut sisi (permukaan datar), rusuk (garis pertemuan dua sisi), dan titik sudut (pertemuan tiga atau lebih rusuk).
• Jaring-jaring Bangun Ruang: Siswa diperkenalkan dengan konsep jaring-jaring, yaitu bentangan dari sisi-sisi bangun ruang yang jika dilipat akan membentuk bangun ruang tersebut. Ini membantu visualisasi bagaimana bangun ruang tersusun.
• Volume Bangun Ruang (Konsep Dasar): Pengenalan konsep volume biasanya dilakukan dengan menghitung berapa banyak kubus satuan yang dapat mengisi penuh bangun ruang tersebut. Pengenalan rumus volume formal (misalnya, V=s x s x s untuk kubus) mulai diperkenalkan.
• Luas Permukaan Bangun Ruang (Konsep Dasar): Siswa dapat dikenalkan pada luas permukaan dengan membayangkan "membungkus" seluruh permukaan bangun ruang. Menghitung luas permukaan secara formal dengan rumus mungkin baru di kelas yang lebih tinggi, namun pemahaman konsepnya bisa dimulai.

Contoh Soal Bangun Ruang Kelas 3 Beserta Pembahasan:

Soal 6 (Identifikasi dan Sifat):
Perhatikan benda-benda di bawah ini:
a. Dadu
b. Kaleng minuman
c. Buku tulis
d. Topi ulang tahun
Sebutkan bangun ruang yang paling menyerupai benda-benda tersebut!

• Pembahasan:
  a. Dadu menyerupai Kubus.
  b. Kaleng minuman menyerupai Tabung.
  c. Buku tulis menyerupai Balok.
  d. Topi ulang tahun menyerupai Kerucut.

Soal 7 (Sisi, Rusuk, Titik Sudut Kubus):
Berapa jumlah sisi, rusuk, dan titik sudut pada bangun ruang kubus?

• Pembahasan:
  Kubus memiliki:
  • 6 sisi (semuanya berbentuk persegi).
  • 12 rusuk (semuanya sama panjang).
  • 8 titik sudut.

Soal 8 (Sisi, Rusuk, Titik Sudut Balok):
Sebuah balok memiliki bentuk seperti kotak sepatu.
a. Berapa jumlah sisi pada balok?
b. Berapa jumlah rusuk pada balok?
c. Berapa jumlah titik sudut pada balok?

• Pembahasan:
  Balok memiliki sifat yang sama dengan kubus dalam hal jumlah sisi, rusuk, dan titik sudut:
  a. 6 sisi (berbentuk persegi panjang).
  b. 12 rusuk (terdiri dari 3 pasang panjang yang berbeda).
  c. 8 titik sudut.

Soal 9 (Jaring-jaring):
Gambar di bawah ini adalah sebuah jaring-jaring. Jika jaring-jaring ini dilipat, bangun ruang apakah yang akan terbentuk?

• Pembahasan:
  Jaring-jaring tersebut jika dilipat akan membentuk Kubus.

Soal 10 (Volume dengan Kubus Satuan):
Sebuah akuarium berbentuk balok diisi dengan kubus-kubus kecil berukuran 1 cm³. Jika akuarium tersebut dapat memuat 120 kubus satuan, berapa volume akuarium tersebut?

• Pembahasan:
  Volume akuarium adalah jumlah kubus satuan yang dapat memuatnya.
  Volume = 120 cm³.

Soal 11 (Membedakan Permukaan Bangun Ruang):
Bangun ruang manakah yang memiliki permukaan datar dan permukaan melengkung?

• Pembahasan:
  • Tabung: Memiliki 2 permukaan datar (alas dan tutup) dan 1 permukaan melengkung (sisi tegak).
  • Kerucut: Memiliki 1 permukaan datar (alas) dan 1 permukaan melengkung (selimut).

Bagian 3: Tips Efektif Membantu Siswa Kelas 3 Menguasai Bangun Datar dan Bangun Ruang

1. Gunakan Benda Nyata: Pembelajaran konsep abstrak seperti bangun datar dan bangun ruang akan jauh lebih mudah jika dikaitkan dengan benda-benda di sekitar siswa. Ajak siswa mengamati benda di kelas, di rumah, atau di luar ruangan dan identifikasi bentuknya.
2. Visualisasi dan Manipulasi:
   • Untuk Bangun Datar: Gunakan kertas lipat, gunting, dan penggaris untuk membuat berbagai bangun datar. Siswa dapat memotong dan menempelkannya.
   • Untuk Bangun Ruang: Gunakan balok mainan, kardus bekas yang dibongkar menjadi jaring-jaring, atau bahkan plastisin untuk membuat model bangun ruang. Membongkar kardus menjadi jaring-jaring sangat membantu pemahaman tentang struktur bangun ruang.
3. Fokus pada Sifat Dasar: Di kelas 3, fokus utama adalah pada identifikasi, jumlah sisi, rusuk, dan titik sudut. Jangan terlalu membebani siswa dengan rumus-rumus yang kompleks.
4. Gunakan Permainan: Permainan seperti tebak bentuk, mencocokkan gambar bangun dengan namanya, atau lomba membuat bangun ruang dari stik es krim dapat membuat belajar menjadi menyenangkan.
5. Soal Cerita yang Kontekstual: Buat soal cerita yang relevan dengan kehidupan sehari-hari siswa. Misalnya, menghitung keliling kebun kakek, menghitung jumlah ubin di lantai kelas, atau berapa banyak bola yang bisa dimasukkan ke dalam kotak.
6. Latihan Berulang dan Bertahap: Berikan latihan yang bervariasi, mulai dari yang paling sederhana hingga yang sedikit lebih menantang. Pastikan siswa menguasai satu konsep sebelum melanjutkan ke konsep berikutnya.
7. Libatkan Orang Tua: Berikan pemahaman kepada orang tua mengenai materi yang diajarkan agar mereka dapat mendukung proses belajar anak di rumah.

Kesimpulan

Memahami bangun datar dan bangun ruang adalah langkah awal yang krusial bagi siswa kelas 3 dalam membangun pemahaman matematika yang lebih luas. Dengan pendekatan yang tepat, penggunaan benda nyata, visualisasi yang baik, serta latihan yang terstruktur, siswa dapat menjelajahi dunia bentuk ini dengan rasa ingin tahu dan percaya diri. Guru dan orang tua berperan penting sebagai fasilitator yang membimbing mereka untuk mengenali, memahami, dan bahkan mengaplikasikan konsep-konsep geometri dalam kehidupan sehari-hari.

Semoga artikel ini memberikan panduan yang komprehensif dan bermanfaat dalam mendampingi siswa kelas 3 dalam belajar bangun datar dan bangun ruang.

Catatan:

• Anda perlu menambahkan gambar-gambar yang relevan untuk soal-soal visual (misalnya, gambar bangun datar untuk Soal 1, jaring-jaring kubus untuk Soal 9).
• Jumlah kata artikel ini sudah mendekati 1.200 kata. Jika perlu penambahan, Anda bisa memperluas penjelasan tentang sifat-sifat setiap bangun, memberikan lebih banyak variasi contoh soal, atau membahas lebih detail tentang aplikasi bangun datar dan bangun ruang dalam kehidupan sehari-hari.
• Format PDF akan didapat setelah Anda menyimpan atau mengekspor dokumen ini dari aplikasi pengolah kata Anda.